【平面几何】四定点一切线确定圆锥曲线
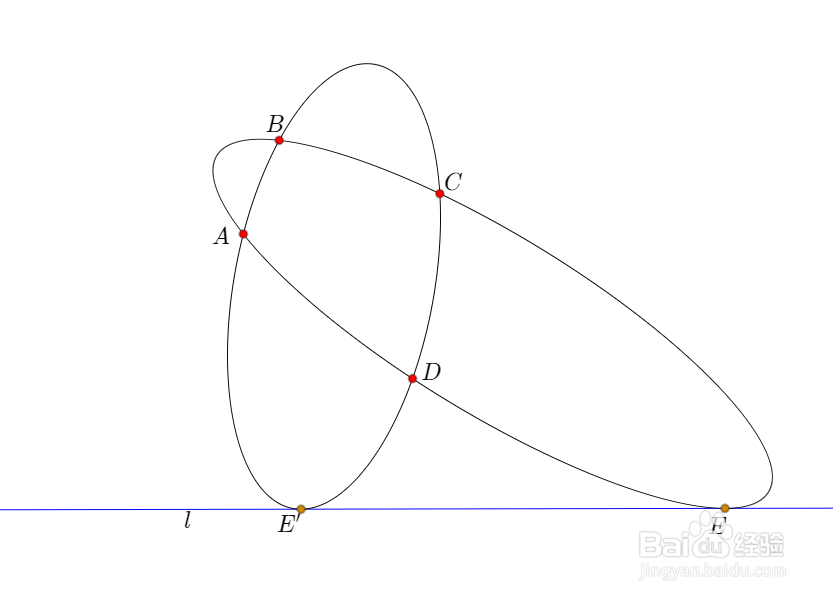
平面上,给定直线l,给定任意三点不共线的四个定点A、B、C、D,求作圆锥曲线u,使之经过A、B、C、D四点,且与直线l相切。

工具/原料
电脑
网络画板
互联网
简单情形
1、如果A、B、C、D四点,恰好有一点位于直线l上,比如D,那么圆锥曲线u就被唯一确定了,如下图的椭圆。

2、这个作图题,其实是简撮劝丛食单的,下面是作图步骤:直线AB与l交于T;在线段CD上取非端点的点U;直线TU和BC交于V;直线AU和DV交于E,那么A、B、C、D、E五点确定唯一的圆锥曲线,就是所求作的u。
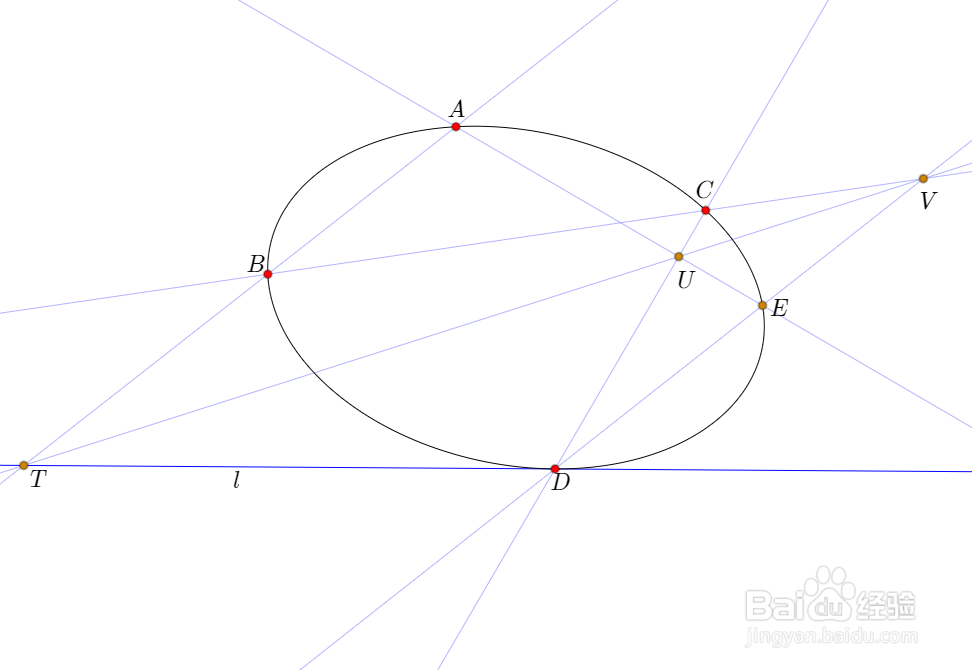
3、然而,这个问题所要考察的一般问题是,A、B、C、D四点都不在直线l上。这才是本文的主要问题。
复杂问题
1、直线l不经过A、B、C、D任意一点,那么所要作的圆锥曲线一般有两条。下面详细地介绍作图方法。
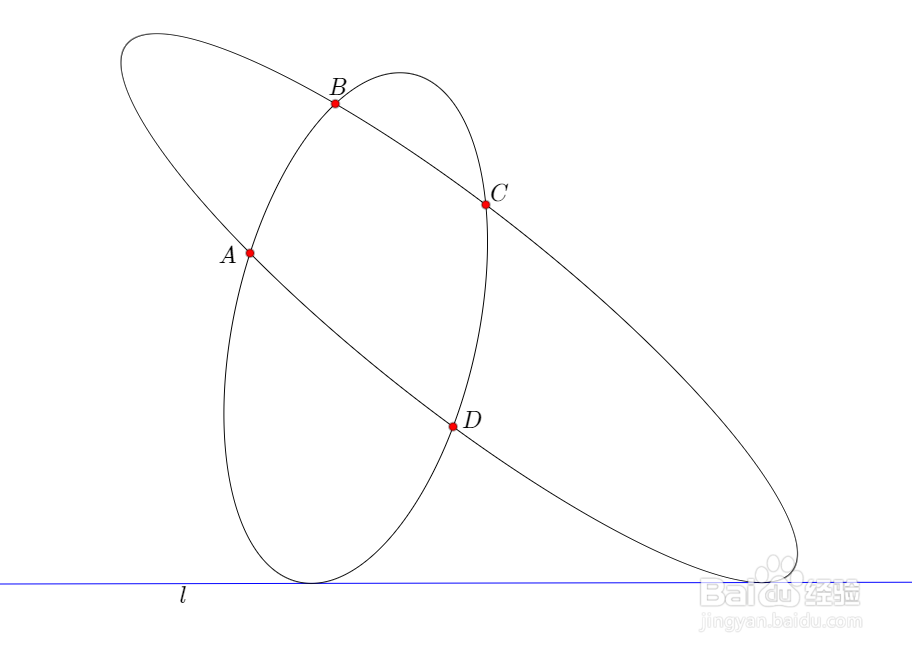
2、已经声明过,A、B、C、D四点的任意三点不共线,那么先作经过A、B、C三点的圆v。

3、连接直线AB、BC、CD、DA,与l分别有交点T、U、T'、U'。
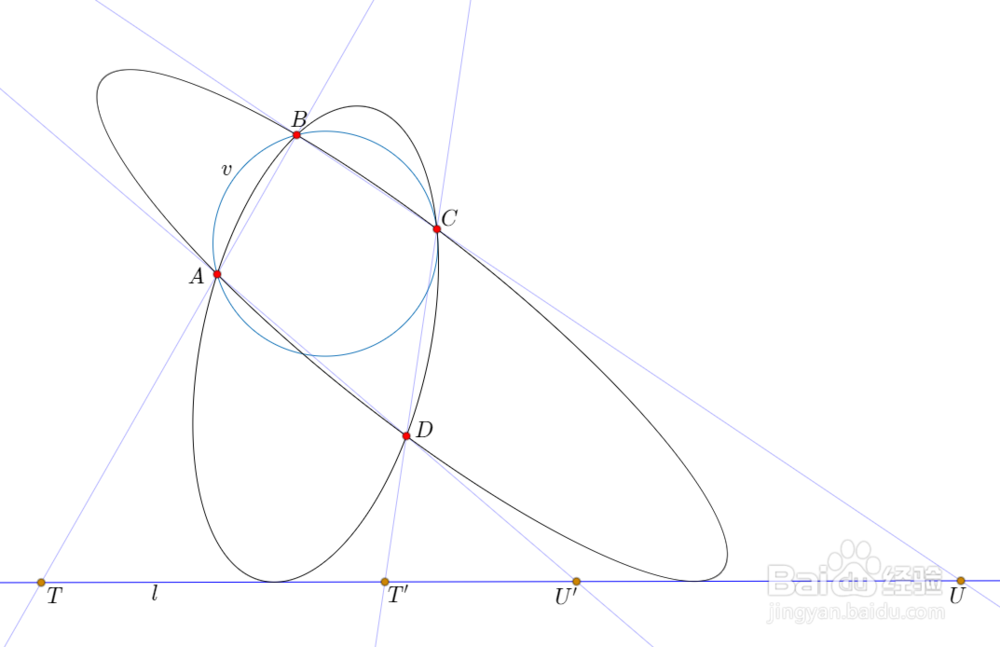
4、连接直线BT',与圆v交于异于B的点T'';连接直线BU',与圆v交于异于B的点U''。

5、连接直线AU''挢旗扦渌;、CT'',交点为M;连接直线AC、T''U'',交点记为N。

6、直线MN与圆v交于P、P'。如果直线MN与圆v没有交点,就表示所求作的圆锥曲线不存在。

7、直线BP与l的交点E,是圆锥曲线u与l的可能切点;直线BP'与l的交点E',是圆锥曲线u与l的另一个可能切点。这样,作出的圆锥曲线u一般有两个:ABCDE确定一个,ABCD呶蓟鹭毵E'确定一个;五点确定圆锥曲线,可以通过网络画板一步搞定。

8、两个圆锥曲线,可能是椭圆、抛物线、双曲线,或者交错存在的。

9、还有的时候,不存在满足要求的圆锥曲线。
