cosarctanx=
令a=arctanx巳呀屋饔,则x=tana
cosarctanx=cosa=√(1-sin²a)
上式两边同除cosa得到
1=√[(1-s足毂忍珩in²a)/cos²a]
=√(1/cos²a-tan²a)
=√(1/cos²a-x²)
化简即可得cosa=1/√(1+x²)
倒数关系: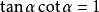 ;
;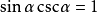 ;
;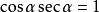
商数关系: ;
;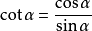 .
.
平方关系: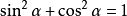 ;
;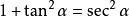 ;
;

扩展资料:
诱导公式口诀“奇变偶不变,符号看象限”意义:
k×π/2±a(k∈z)的三角函数值。
(1)当k为偶数时,等于α的同名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号;
(2)当k为奇数时,等于α的异名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号。
六边形的六个角分别代表六种三角函数,存在如下关系:
1)对角相乘乘积为1,即sinθ·cscθ=1; cosθ·secθ=1; tanθ·cotθ=1。
2)六边形任意相邻的三个顶点代表的三角函数,处于中间位置的函数值等于与它相邻两个函数值的乘积,如:sinθ=cosθ·tanθ;tanθ=sinθ·secθ...
3)阴影部分的三角形,处于上方两个顶点的平方之和等于下顶点的平方值,如: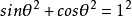 ;
;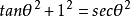 ;
;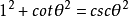 。
。
参考资料:百度百科——三角函数