幂指函数导数计算应用举例

1、幂指函数y=sinx^cosx的导数计算。导数的本质是通过极限的概念对函数进行局部的线性逼近。

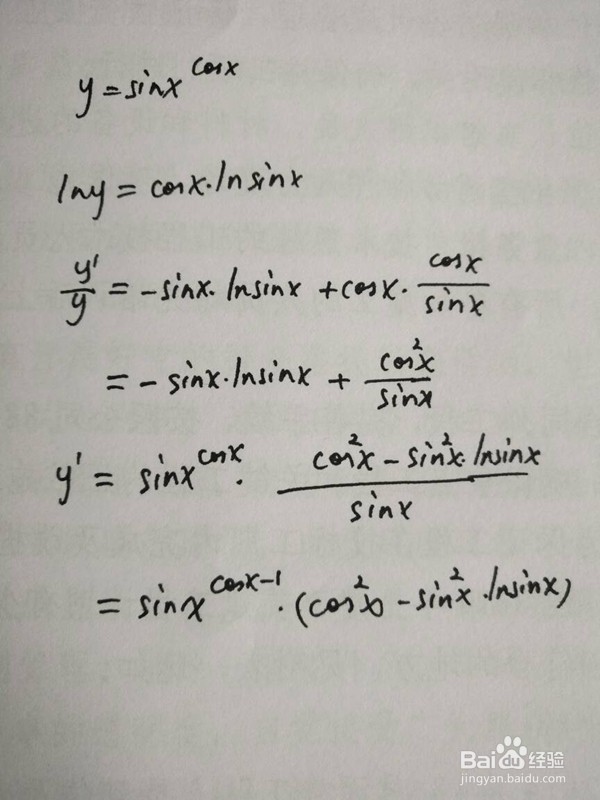
2、导数也叫导函数值。又名微商，是微积分中的重要基础概念。当函墙绅褡孛数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f’（x0）或df（x0）/dx。

3、幂指函数y=(tan2x)^(cosx/2)的导数计算。

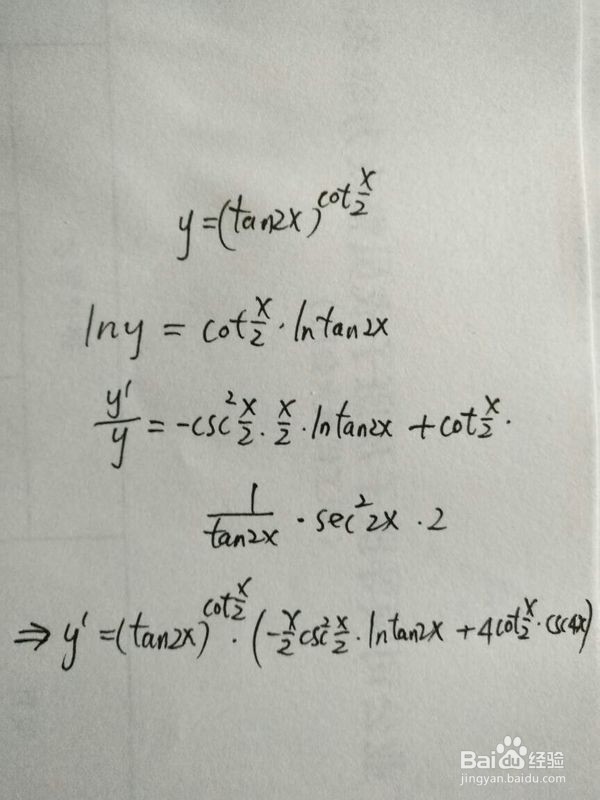
4、不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。

5、幂指函数隐函数x^y=x^y的导数计算。

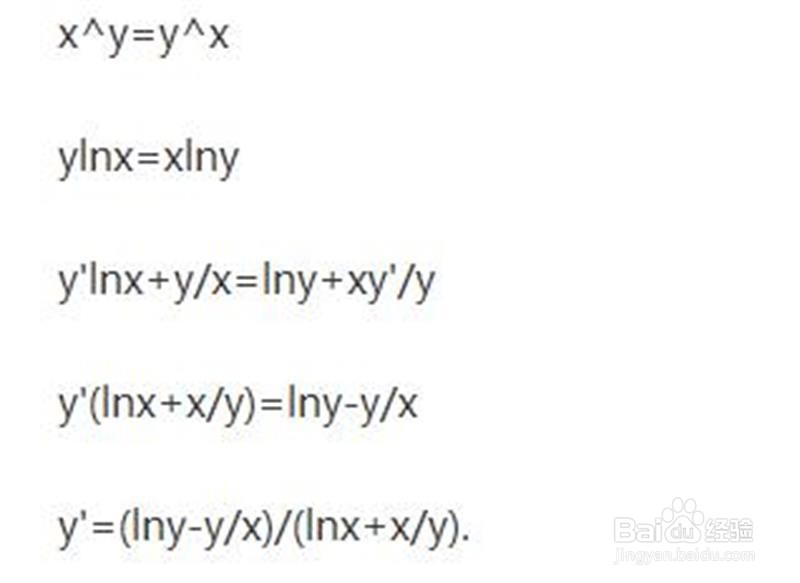
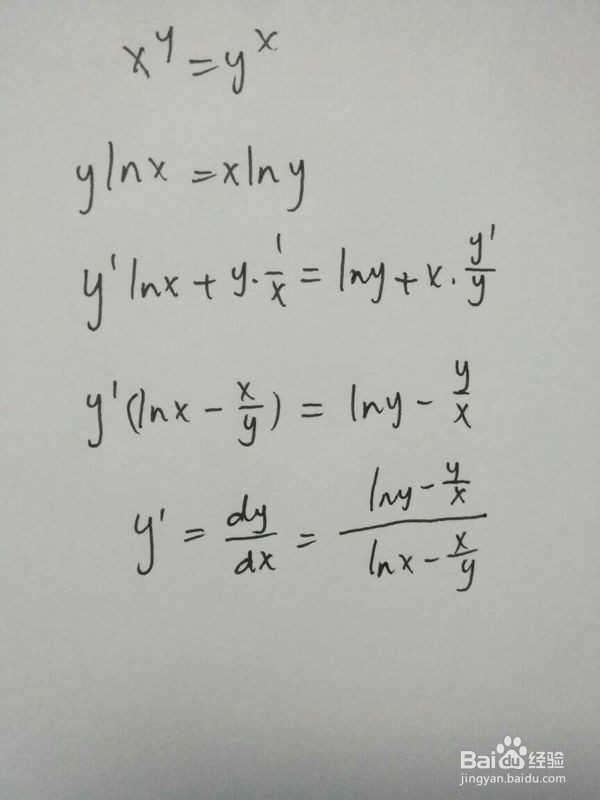
6、幂指函数y=x^sinx的导数计算。

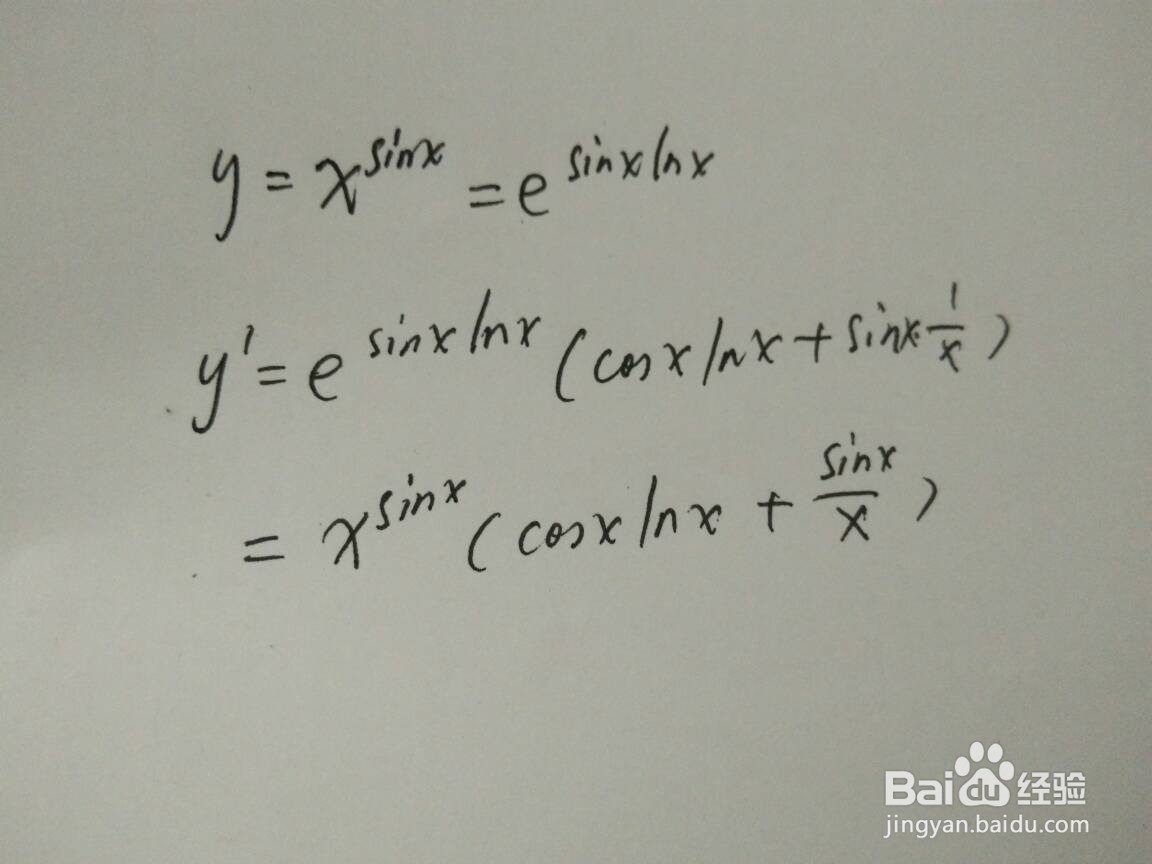
7、导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

8、幂指函数y=（1+x）^sinx的导数计算。