本性奇点怎么判断
1、首先、如果函数在孤立奇点b的一个去心邻域内展开成洛朗级数,其中含有无穷多个(z-b)的负幂项,则把b点称为的本性奇点。

2、接着、这与前面的定义是一致的,因为如果 时函数 在b点邻域内展成的洛朗级数含有有限个(z-b)的负幂次项。
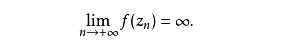
3、那么,若在b点的洛朗展开式含有无穷多个(z-b)的负幂次项,则极限必然不存在,而这正是前面给出的本性奇点定义。

4、例如,函数,当z=0时它的值不确定,然而在z=0的邻域内解析,所以z=0是的孤立奇点。它展开的幂级数为含有无限多个负幂项,所以z=0是它的本性奇点。
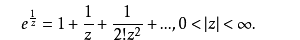
5、又如,z=1是函数的孤立奇点,当时,该函数的极限不存在,所以z=1是该函数的本性奇点。也可以在环域内将该函数展开成洛朗级数可见,上式有无穷多个(1一z)的负幂项。所以z=1就是该函数的本性奇点。
