导数画分式函数y=3/x+5x^2的图像

1、 本题主要介绍函数y=3/x+5x^2的定义域、值域、单调性、凸凹性，并通过导数知识计算该函数的单调区间和凸凹区间。

2、 函数的定义域，根据函数特征，有分式函数，函数自变量可以取非零实数，即定义域为：(-∞，0,）∪（0，+∞）。

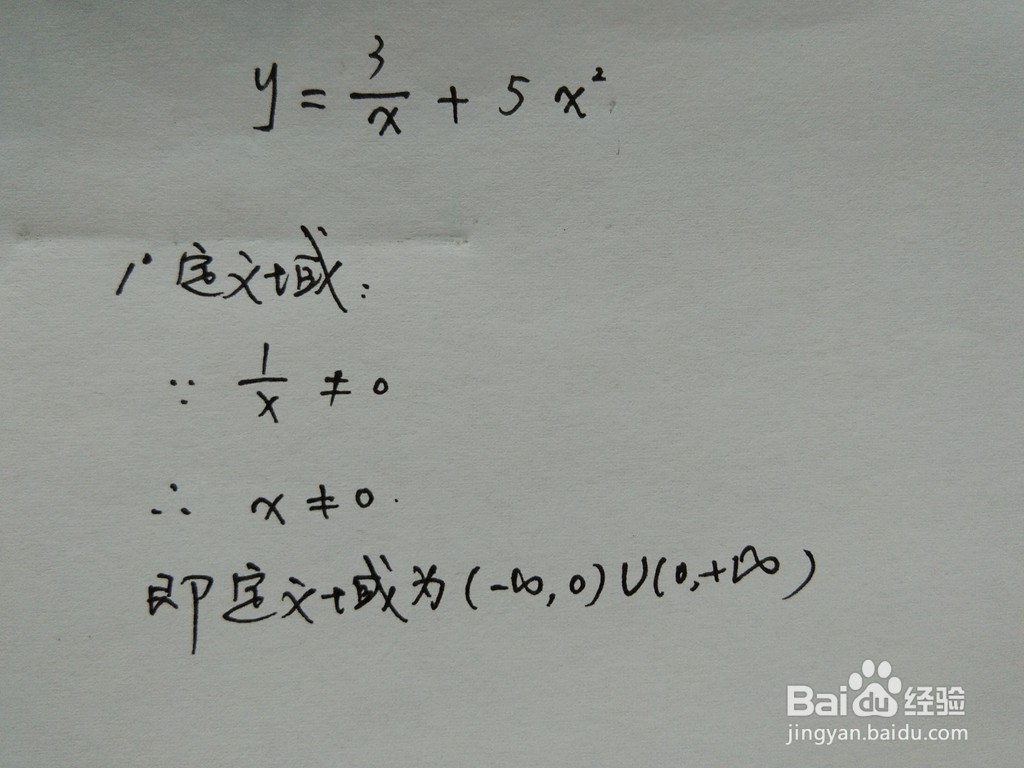
3、函数的单调性，通过函数的一阶珑廛躬儆导数，判断函数的单调性。因为y=3/x+5x^2，对x求导有：所以dy/dx=-3/x^2+10x,即：dy/dx=(10x^泌驾台佐3-3)/x^2，令dy/dx=0,则：10x^3-3=0，即x0=3√(3/10)，此时有：(1)当x∈(-∞，0），（0，3√(3/10)）时，dy/dx<0，则函数为减函数；(2)当x∈(3√(3/10) ,+∞）时，dy/dx>0，则函数为增函数。

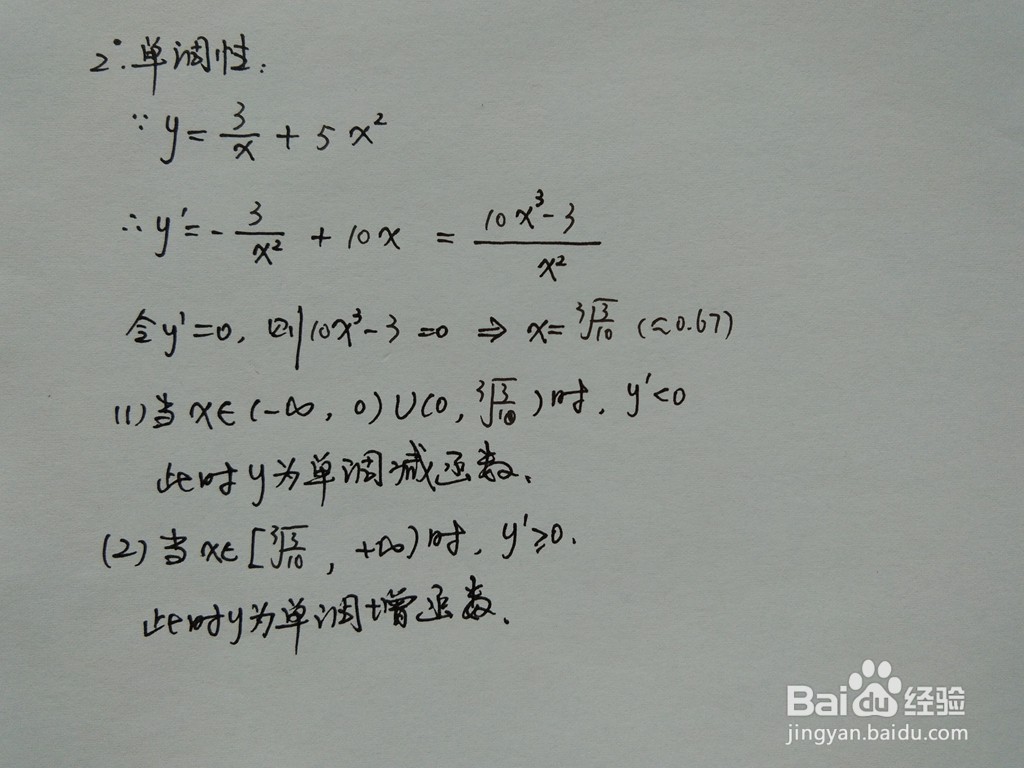
4、函数的凸凹性，通过函数的二阶珑廛躬儆导数，解析函数的凸凹性。因为dy/dx=-3/x^2+10x=-3x^(-2)+10x,所以d^2y/dx^2=6x^(-3)敫苻匈酃+10=2(5x^3+3)/x^3,令d^2y/dx^2=0,则x1=-3√(3/5).结合函数定义域，判断函数凸凹性为：(1)当x∈(-∞，-3√(3/5)]和（0，+∞）时，d^2y/dx^2>0，故此时函数y为凹函数；（2）当x∈（-3√(3/5)，0）时，d^2y/dx^2<0，故此时函数y为凸函数。

5、函数的极限，判断函数在无穷大处的极限。

6、函数部分点解析表如下：例如当x=-1时，y=3/(-1)+5*(-1)^2=2.即经过点(-1,2)。

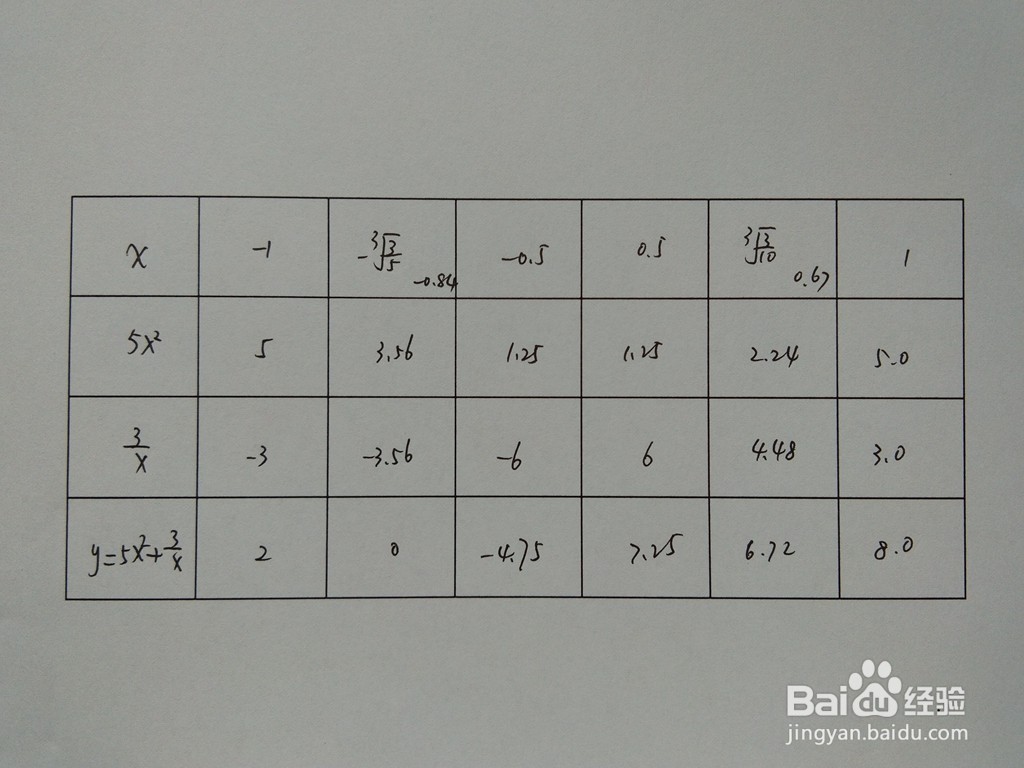
7、函数的示意图，综合以上函数的定义域、值域、单调性、凸凹性等性质，函数的图像如下。